本記事の概要
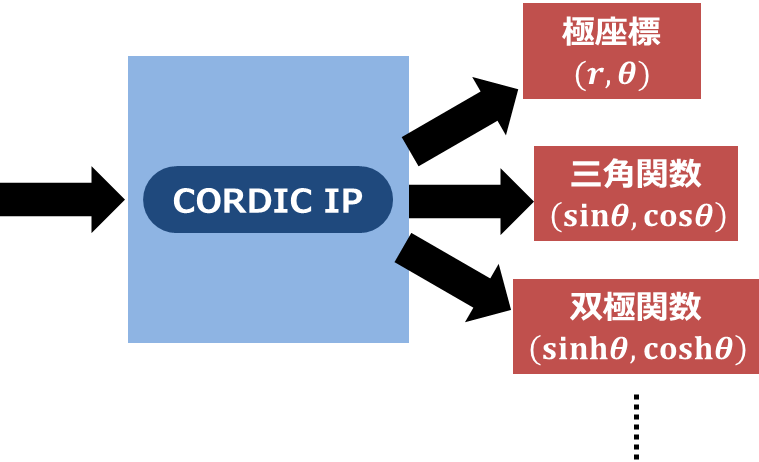
Xilinx社のFPGAでは、三角関数や平方根を扱うためのIPコアCORDIC IPが提供されています。
CORDIC IPは、CORDIC (COordinate Rotation DIgital Computer)アルゴリズムを利用して、三角関数の計算を行うだけでなく、双極型方程式や平方根を含む方程式を解くように改良されている、大変便利なIPです。
- Vector Rotation :ベクトルの回転。 ベクトル\( (x, y)\)を角度\(\theta\)だけ回転させたベクトル\( Z_n \times (x’, y’)\)を出力
- Vector Translation : 直交座標から極座標への変換。ベクトル\((x, y)\)から絶対値\(Z_n\times r \)と位相\(\theta = \arctan (y/x)\)を出力
- Sin and Cos : 三角関数の計算。位相\(\theta\)から三角関数 \(\sin\theta, \cos\theta\)を出力
- Sinh and Cosh: 双極関数の計算。位相\(\theta\)から双極関数\(\sinh \theta, \cosh \theta\)を出力
- Arc Tan : ベクトル\((x, y)\)から位相 \(\theta = \tan^{-1} (y/x) \)を出力
- Arc Tanh : ベクトル\((x, y)\)から双極角 \(\theta = \tanh^{-1} (y/x)\)を出力
- Square Root : 非負数\(x\)の平方根\(\sqrt{x} \)を出力
ここで、\( Z_n \)はスケーリングファクターと呼ばれるものです。
筆者はかつてCORDIC IPを使用したシステムを開発中に、上述したスケーリングファクター\( Z_n \)の存在を知らずに、所望の出力が得られず小一時間悩んでしまいました。

IPを使うときには、きちんとリファレンスシートを確認する必要がありますね(笑)
他にも悩んでいる人がいるかもしれないので、記事にまとめておこうと思いました。
スケーリングファクターの意味を理解するためには、まずは基本となるCORDICアルゴリズムを理解しておくのが良いと思います。
数回に渡って、Xilinx CORDIC IPの使用方法についてまとめていきますが、まずはその前提となるCORDICアルゴリズムについて抑えておくべきポイントを本記事にまとめていきたいと思います。
CORDICアルゴリズムでは、回転角\(\theta\)だけ回転させた複素数\(z’= x’+iy’\)を、以下のようにして数値的に近似する:
- マイクロ回転の回転角\(\theta_i (i=0,1,2,\cdots, n)\)を\( \arctan \left(\frac{1}{2^i} \right) \)となるように選ぶ。
- 所望の回転角\(\theta\)をマイクロ回転角\(\theta_i (i=0,1,2,\cdots, n)\)の総和に分解。
- 回転前の複素数\(z = x+iy \)に、マイクロ回転の回転子\(\beta(\theta_i) (i=0,1,2,\cdots, n)\)を繰り返し乗じて、回転後の複素数\(z’_{スケール補正前} = x’_{スケール補正前}+iy’_{スケール補正前} \)を得る。
ただし、以下の点に注意が必要である:
- マイクロ回転の回転子\(\beta(\theta_i) (i=0,1,2,\cdots, n)\)は絶対値が1でないため、回転だけでなく、拡大縮小というスケール変化が伴うので、スケーリングファクターの逆数を最後の乗じなければならない。
- スケーリングファクター\(Z_n\)は、繰り返し数\(n\)のみの関数で、\(n\)が十分大きければ一定値に収束する(\(Z_n\simeq 1.64676…\))。
- FPGA上で三角関数や平方根の計算を使用したロジックを組みたいエンジニア
- CORDICアルゴリズムのエッセンスを勉強したい方

それでは、興味のある方はぜひ最後までご覧ください!
CORDICアルゴリズム
計算の目標
本記事の目標は次の通りです:
CORDICアルゴリズムのエッセンスである、
ベクトル\((x,y)\)を角度\(\theta\)だけ回転させたベクトル\((x’, y’)\)を
数値的に得る方法を理解すること。
ベクトルの回転は行列を用いて計算することもできますが、以下では複素平面における複素数\(z = x+iy \)の回転をベースに説明していきます。

複素平面上での回転は、絶対値が1の複素数の掛け算で与えられます。例えば、複素数\(z = x+iy \)を角度\(\theta\)だけ回転させた複素数\(z’ = x’+iy’ \)は以下のようにして計算することが可能です。
$$ z’ = ( \cos\theta + i\sin\theta ) z$$

以上が、問題設定です。
では、CORDICアルゴリズムを見ていきましょう。
ポイント1 : マイクロ回転\(\theta_i\)の準備
まず、CORDICアルゴリズムでは、角度\(\theta\)の回転を微小な回転に分解して、少しずつ微小な回転を繰り返して所望の角度\(\theta\)まで回転させていきます。
この微小な回転をマイクロ回転(Xilinxのリファレンスシートではmicro-rotation)と呼び、その回転角を順に\(\theta_i (i=0,1,2,\cdots, n)\)としていきます。

CORDICアルゴリズムにおけるマイクロ回転では、
1回目の回転は\(\theta_1\)、2回目の回転は\(\theta_2\)、3回目の回転は\(\theta_3\)、…というふうに、回転角の大きさを変えていきます。
1つ目のポイントは、このマイクロ回転の回転角\(\theta_i (i=0,1,2,\cdots, n)\)の決め方にあります。
\(\theta_i\)は\( \arctan \left(\frac{1}{2^i} \right) \)となるように選ぶ。
\(\arctan\)や\(2^i\)が出てきて複雑な決め方に見えますが、実はこのように決めておくとマイクロ回転がビットのシフトだけで実行できて、処理がめちゃくちゃ簡単になるのです。
角度の決め方がわかりにくいので、図を使って確認しましょう。
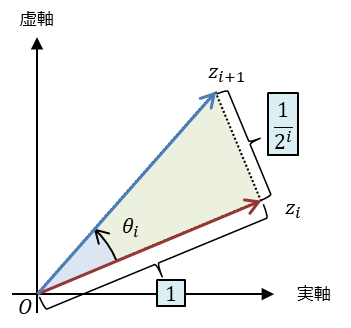
マイクロ回転前の複素数を\(z_i \)、回転後の複素数を\(z_{i+1} \)とします。
マイクロ回転の回転角\(\theta_i\)は、\( \arctan \left(\frac{1}{2^i} \right) \)となるように選んでいるので、回転角\(\theta_i\)は図のような隣辺と対辺の比が\(1 : \left(\frac{1}{2^i} \right)\)の直角三角形の一つの鋭角になります。
図を用いて計算してみると、マイクロ回転前の複素数\(z_i \)と回転後の複素数\(z_{i+1} \)の関係が、
$$ z_{i+1} = \left( 1 + \frac{i}{2^i} \right) \times z_i $$
となることがわかります。
以下では、このような角度\(\theta_i\)だけのマイクロ回転を行うときに掛ける複素数を回転子と呼び、\(\beta (\theta_i) \)としておきましょう:
$$ \beta (\theta_i) = 1 + \frac{i}{2^i}$$

あれ!?
この複素数を掛けると、回転だけでなくベクトルの長さ(複素数の絶対値)も変わってしまわない?
はい、マイクロ回転の回転子\(\beta (\theta_i) \)は絶対値が1でない複素数を乗じているので、回転だけではなくベクトルの拡大・縮小も伴います。これがスケーリングファクター\( Z_n \)が最終的に乗じられる理由です。
\(\beta (\theta_i) = 1 + \frac{i}{2^i}\)の掛け算は、1と2のべき乗の割り算だけで構成されるため、ビットのシフト(2進数の桁上り・桁下がりのこと;2の掛け算とわり算)と足し算・引き算のみで実行でき、処理が非常に簡単になります。しかし、回転のたびに余計なスケーリングファクターが乗じられるのですが、このスケール調整をマイクロ回転ごとに行うと、掛け算の処理が含まれ、処理の効率が下がります。そこで、各々のマイクロ回転ではスケールの調整は行わず、一番最後にそのファクター分、ベクトルの大きさを調整することにしています。

繰り返しが必要なマイクロ回転では比較的処理が軽いビット演算のみで実行し、
最後の最後で全体の絶対値の帳尻合わせをしていくという訳ですね。
マイクロ回転を用いるメリットと注意点をまとめておきましょう。
マイクロ回転はビットのシフトと足し算のみで実行できるので処理が非常に簡単
マイクロ回転の回転子\(\beta (\theta_i) \)は絶対値が1でないため、回転だけでなくベクトルの拡大と縮小も行われる。
ポイント2:\(\theta\)の回転をマイクロ回転\(\theta_i\)の和に分解
では、マイクロ回転の回転角を決めたので、所望の回転角\(\theta\)をマイクロ回転角の和に分解して、少しずつマイクロ回転を繰り返しながら所望の角度\(\theta\)まで回転させましょう。
「そもそも和に分解して収束するのか?」という疑問はありますが、直感的には和で近似できるのかなという雰囲気だけをイメージしていただければと思います。
マイクロ回転の回転角は、図のような単調減少する数列になっています。
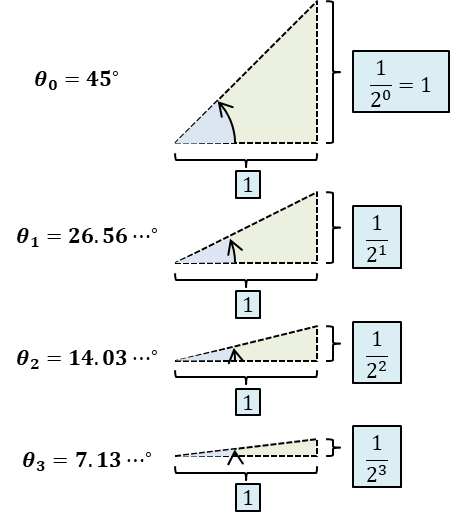
厳密な数学の証明方法は省略しますが、
- 所望の回転角\(\theta\)まで\(\theta_i\)を足していき、
- 所望の回転角\(\theta\)を上回ったら、次の\(\theta_i\)からは引いていき、
- また回転角\(\theta\)を下回ったら、次の\(\theta_i\)からは足していく、…
というのを繰り返していけば、回転角\(\theta\)をマイクロ回転\(\theta_i\)の和に近似できる気がしてきます。
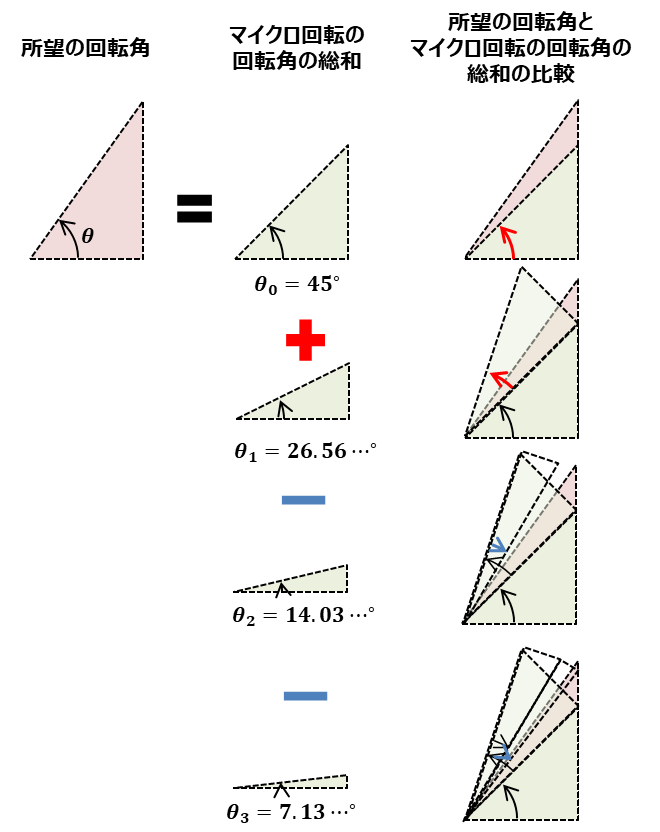
足したり、引いたりを繰り返していくわけですが、足す場合を\(\alpha_i = +1\)、引く場合を\(\alpha_i = -1\)として、変数\(\alpha_i\)を便宜上定義しておきます。
以上のようにして、マイクロ回転の回転角\(\theta_i (i=0,1,2,\cdots, n)\)で、所望の回転角\(\theta\)を分解していきます。
\(\theta\)をマイクロ回転の回転角\(\theta_i\)の総和で近似する:
$$ \theta \simeq \sum^n_{i=0} \alpha_i \theta_i $$
ただし、\(n\)は繰り返し計算数、\(\alpha_i\)は\(\pm 1\)のいずれかの値をとる「回転方向を表す因子」である。
ポイント3:マイクロ回転\(\theta_i\)を繰り返して\(\theta\)の回転を実行
最後に、マイクロ回転の回転子を繰り返しベクトル\((x,y)\)に乗じていけば、ベクトル\((x’, y’)\)を数値的に得ることが可能です。
ただし、ポイント1で述べた注意点「マイクロ回転の回転子は絶対値が1でないため、拡大と縮小も伴う」という点を考慮すると、マイクロ回転の回転子を繰り返しベクトル\((x,y)\)に乗じたものは、所望のベクトルの向きしか一致していないことに気づくと思います。
そこで、この向きだけ一致している複素数を\(z’_{スケール補正前} = x’_{スケール補正前}+iy’_{スケール補正前} \)と読んでおきます。
複素数\(z’_{スケール補正前} = x’_{スケール補正前}+iy’_{スケール補正前} \)を、複素数\(z = x+iy \)にマイクロ回転の回転角\(\theta_i\)を繰り返し乗じたもので数値的に近似する:
$$ z’_{スケール補正前} \simeq \prod^n_{i=0} \beta(\alpha_i\cdot\theta_i) z = \prod^n_{i=0} \left(1 +\alpha_i\cdot \frac{i}{2^i}\right) z$$
ただし、\(n\)は繰り返し計算数、\(\alpha_i\)は\(\pm 1\)の回転方向を表す因子である。

以上で、ベクトル(複素数)を数値的に回転することができました。
しかし、忘れてはいけないのが、ポイント1で述べた注意点「マイクロ回転の回転子は絶対値が1でないため、拡大と縮小も伴う」という点です。
結局、スケーリングファクター\( Z_n \)とは…

図のように、\(z’_{スケール補正前} = x’_{スケール補正前}+iy’_{スケール補正前} \)はマイクロ回転を行うたびに絶対値が変わり、角度\(\theta\)の回転と同時に、あるスケール分の拡大が行われています。
このスケールをスケーリングファクター\(Z_n\)と呼びます。
\(z’_{スケール補正前} \)と所望の\( z’\)の間には\( z’_{スケール補正前} = Z_n \times z’\)という関係式が存在します。
そのスケーリングファクター\(Z_n\)はマイクロ回転の回転子\(\beta(\alpha_i\cdot\theta_i)\)の絶対値の積で計算できます。
回転に伴う拡大縮小のスケーリングファクター\(Z_n\)はマイクロ回転の回転子\(\beta(\alpha_i\cdot\theta_i)\)の絶対値の積で与えられる:
$$Z_n = \prod^n_{i=0} |\beta(\alpha_i\cdot\theta_i)| = \prod^n_{i=0} \sqrt{1+\frac{1}{2^{2i}}} $$
この数は、繰り返し数\(n \)のみに依存しており、繰り返しを増やしていくとある一定値に収束していくことが知られています。
実際、繰り返し数\(n \)に対するスケーリングファクターの依存性はこの通りで、スケーリングファクター\(Z_n\)は繰り返し数\(n \)を大きくすると1.64676…に近づいていきます。


スケーリングファクターの存在を知らないと、FPGAからの出力が想定している値に比べて、常に1.65倍くらい大きな値になることになり、四苦八苦することになりますので、ご注意を(笑)
FPGAにCORDIC IPを実装する際は、最後にこのスケーリングファクターの逆数を乗じる必要があります。

CORDIC IPの設定方法や出力値における精度など調査して、継続的に記事にまとめていきますので、今後ともご覧いただければと思います。
ここまで読んでいただき、ありがとうございました。
参考資料
https://japan.xilinx.com/support/documentation/ip_documentation/cordic/v6_0/pg105-cordic.pdf


コメント