CORDIC IPを使ってFPGAで自然対数を計算する方法

本記事の概要
1. 本記事の目標
計算原理
ブロックデザイン例
1. 前準備の自作モジュール logpre
2. CORDIC IPの設定
シミュレーションによるブロックデザインの検証
1. 計算結果
2. 入力値の有効範囲が[1/9, 9]の理由
まとめ
1. 参考資料

本記事の概要

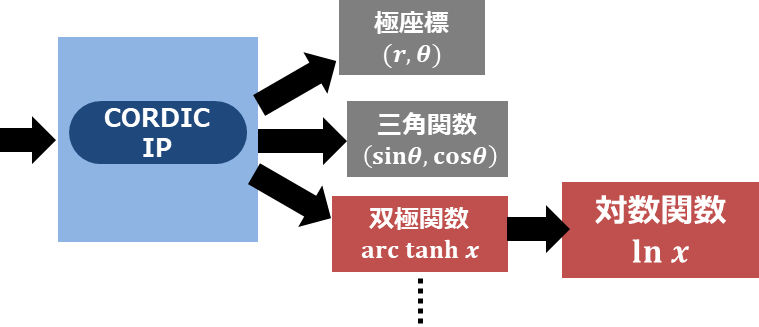
Xilinx社のFPGAでは、三角関数や平方根を扱うためのIPコアCORDIC IPが提供されています。CORDIC IPは、CORDIC (COordinate Rotation DIgital Computer）アルゴリズムを利用して、三角関数の計算を行うだけでなく、双極型方程式や平方根を含む方程式を解くように改良されている、大変便利なIPです。

CORDICの計算原理については、過去に下記記事にまとめてみました。

CORDIC IPの双極型方程式におけるarc tanhをうまく応用することによって、自然対数の計算ができるようでしたので、今回の記事ではCORDIC IPを用いて自然対数を計算するブロックデザインを作成し、Vivadoのシミュレータで計算精度を調べました。

ひがし

それでは、興味のある方はぜひ最後までご覧ください！

本記事の目標

CORDICアルゴリズムを応用し
FPGA上で自然対数を計算するブロックデザインを作成

この記事の対象読者

FPGA上で自然対数の計算を使用したロジックを組みたいエンジニア
CORDIC IPにおけるarc tanhの使用例を見てみたい方

計算原理

CORDIC IPで計算可能なarctanhを用いて、自然対数$ y = \ln (x) $は以下の式で計算することが可能です。

arctanhを用いた自然対数の計算式

$$ y = 2 {\rm arctanh} \left( \frac{x – 1}{x + 1} \right)　\cdots (1) $$

ちなみに、arctanhに馴染みのない方も多いと思いますので、簡単に説明すると…。arctanhとは、双曲線正接関数

$$ \tanh (x) = \frac{e^x – e^{-x}}{e^x + e^{-x}} = \frac{e^{2x} – 1}{e^{2x} + 1} \cdots (2) $$

の逆関数として定義されます。なぜ、上の関数に高校の数学で習ったタンジェントと似たような名前がついているのかという疑問を持つ人もいるかもしれませんが、その説明は本題から逸れる上に長くなるので本記事では省きます。

(１)式の証明方法に興味のある方は以下のコラムをご覧ください。双曲線正接関数の定義に従って式変形をしていけば、自然対数が得られます。

コラム　(１)式の証明

$$ y = 2{\rm arctanh} \left( \frac{x – 1}{x + 1} \right) \Leftrightarrow {\rm tanh} \left( \frac{y}{2} \right) = \frac{x – 1}{x + 1} \Leftrightarrow \frac{e^y – 1}{e^y + 1} = \frac{x – 1}{x + 1} (∵ (2)) $$

$$ \Leftrightarrow x = e^y \Leftrightarrow y = \ln x $$

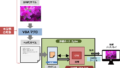
ブロックデザイン例

では、自然対数を計算するFPGAのブロックデザインを示します。
Cordic IPの前に前準備としてlogpreという自作モジュールを接続しました。

前準備の自作モジュール logpre

まず、自作のHDLモジュールlogpreについて説明します。

logpreは、CORDICに入力するX_INとY_INを出力するモジュールです。式(1) におけるarctanhの中の計算を予め行っておきたかったので、X_INが$ {\rm xvalue} – 1 $、Y_INが$ {\rm xvalue} ＋ 1 $となるようにlogpreの中で計算しています。

logpreのVerilogのコード例は以下の通りです。小数部分　下位8bit、整数部分　上位8bitと、xvalueのビット数を定めましたので、1を足したり引いたりする操作は、1の代わりに16’h0100(整数部分が１、小数部分が０)を用いています。

`timescale 1ns / 1ps

module logpre(
     clk
    ,xvalue
    ,valid

    ,s_axis_cartesian_tdata
    ,s_axis_cartesian_tvalid
    );

    localparam  DWIDTH          = 16    ;
//------------------------------------------------------
    input                                   clk                     ;   
    input           [DWIDTH  -1:0]          xvalue                  ;  
    input                                   valid                   ;

    output          [DWIDTH*2-1:0]          s_axis_cartesian_tdata  ;
    output                                  s_axis_cartesian_tvalid ;
//------------------------------------------------------
    wire    signed  [DWIDTH  -1:0]          dividend                ;  
    wire    signed  [DWIDTH  -1:0]          divisor                 ;  

    assign      dividend    = $signed(xvalue) - $signed(16'h0100) ; 
    assign      divisor     = $signed(xvalue) + $signed(16'h0100) ;

    assign      s_axis_cartesian_tdata  = {dividend[DWIDTH-1:0], divisor[DWIDTH-1:0]} ;
    assign      s_axis_cartesian_tvalid = valid ;

endmodule

CORDIC IPの設定

次に、arc tanhを計算するCORDIC IPの設定を見ていきましょう。

CORDIC IPの設定値

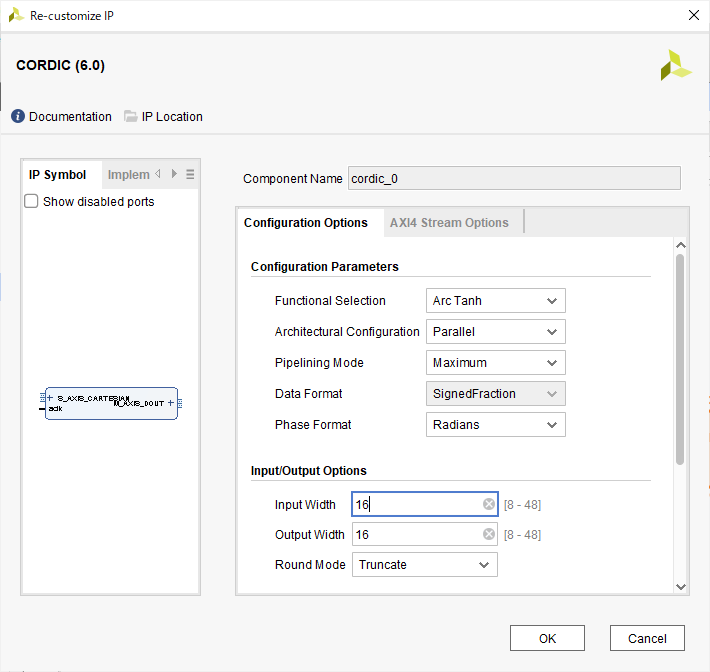
Configuration Parameters
- Functional Selection : Arc Tanh
- Architectural Configuration : Parallel
- Pipelining Mode : Maximum
- Data Format : Signed Fraction
- Phase Format : Radians
Input/Output Options
- Input Width : 16
- Output Width : 16
- Round Mode : Truncate
Advanced Configuration Parameters
- Iterations : 0
- Precision : 0

ひがし

CORDIC IPの設定値は基本的にデフォルトのままです。ポイントは、Functional SelectionをArc Tanhに変更することだけですね。

以上が、作成したブロックデザインになります。では、Vivadoのシミュレータを使って、計算精度はどれくらいか調べてみましょう！

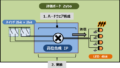
シミュレーションによるブロックデザインの検証

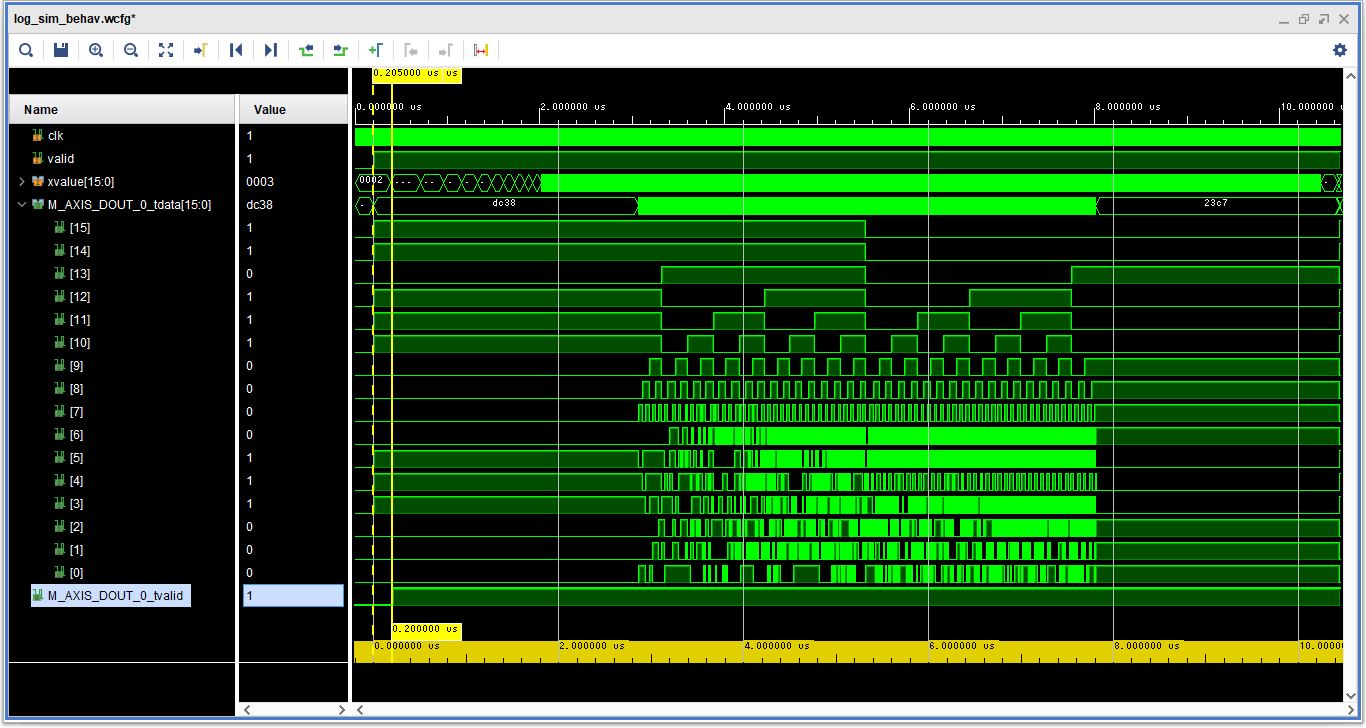
では、テストベンチプログラムを作成し、Vivado上でシミュレーションを行ってみました。テストベンチでは、入力値xvalueを0.01から100まで順次入力し、自然対数の計算結果をdatファイルに出力しました。

シミュレーションのタイミングチャートは上図のようになりました。CORDIC IPのレイテンシーが20クロックですので、ブロックデザイン全体でも自然対数が計算されるまでのレイテンシーは20クロックかかっています。

計算結果

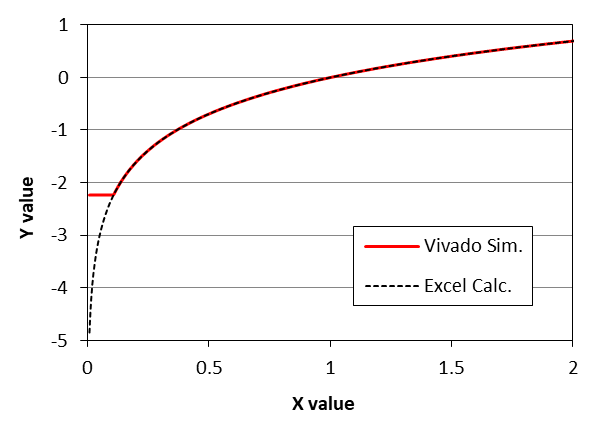
では、datファイルに出力した自然対数をExcelに読み込んで、Excel上で計算した自然対数と比較してみます。

ひがし

入力値xvalueが１の近くではExcelとの違いは見られないんですが、入力値0.1付近より下ではVivadoの計算が全然Excelとあっていませんね。一定値のまま、更新されていません。

ということで、もう少しExcelの計算値との誤差をよく見てみましょう。

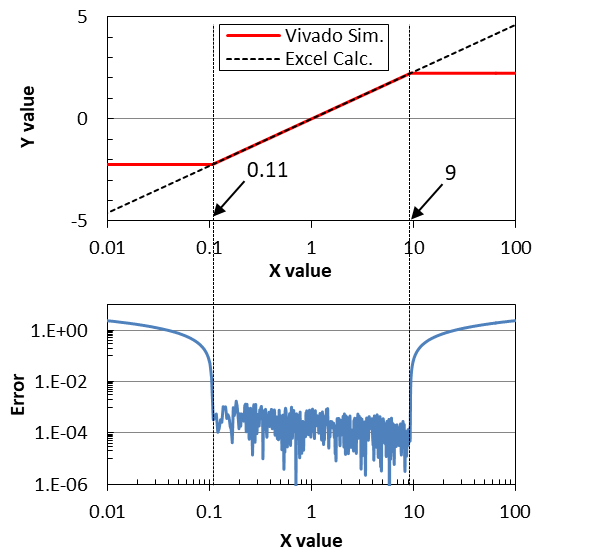
下の図に、先程のVivado Simの出力を、[0.01,100]の範囲で示してみました。ついでに、見やすいように、入力値xvalueに対する片対数表示にしています。そして、Excelの計算値に対する誤差も下に載せています。

0.11~9の範囲(厳密には、1/9~9の範囲)では誤差が$ 10^{-3} $程度でExcelの計算結果と一致しています。しかし、0.11以下と9以上ではFPGAの方の計算が全く変化せず、当たり前ですが誤差はかなり大きくなっています。

入力値の有効範囲が[1/9, 9]の理由

原因を探るために、CORDIC IPのデータシートのArc Tanhに関する記述を見てみましょう。

https://www.xilinx.com/support/documentation/ip_documentation/cordic/v6_0/pg105-cordic.pdfより抜粋

CORDICのアルゴリズムが収束するためには、X_INとY_INに制約条件$- \frac{4}{5} X_{IN} \leq Y_{IN} \leq \frac{4}{5} X_{IN} $が課されています。
計算してみると、この条件はxvalueの有効な範囲が[1/9, 9]になるのと一致します。
そのため、今回の記事で作成したブロックダイアグラムの入力値xvalueが有効な範囲が[1/9, 9]となってしまいました。

ひがし

入力値の有効範囲が限定的なので注意が必要ですね。とはいえ、１近傍では十分自然対数としての機能は果たしてくれそうです。